How paceval. works
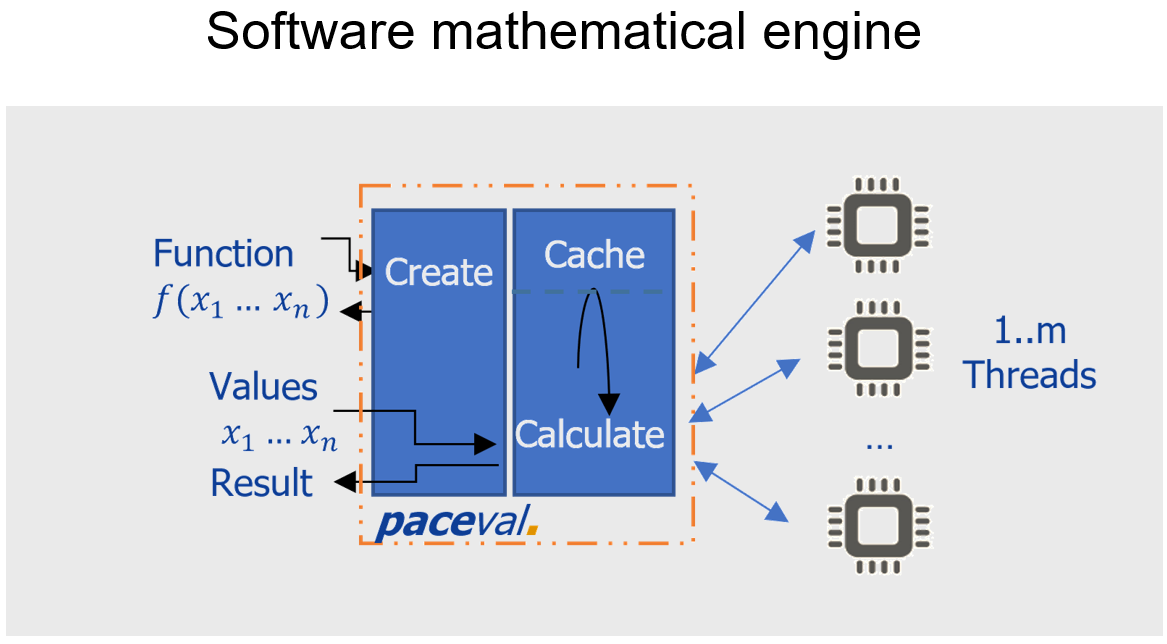
Essentially, there are only two steps: first, a calculation object is created (step „Create“), where the user provides a function and the number of variable identifiers. Then, specific calculations can be made repeatedly using the created object (step „Calculate“), where the user provides values for the variables.
During step „Create“, calculation rules are created through the calculation object and adjusted towards maximum parallelisability. The user receives a unique ID for the created object. You can create any number of calculation objects. There are no limitations as to the function length or the number of variables.
In step „Calculate“, a calculation using the values of the variables is carried out. Here a list of rules as partial sequences is distributed on all available processors („Threads“) of the system to achieve maximum speed. Additionally, the effort consuming calculations of partial sequences that have been already performed are buffered („Cache“) to prevent repeated calculations.
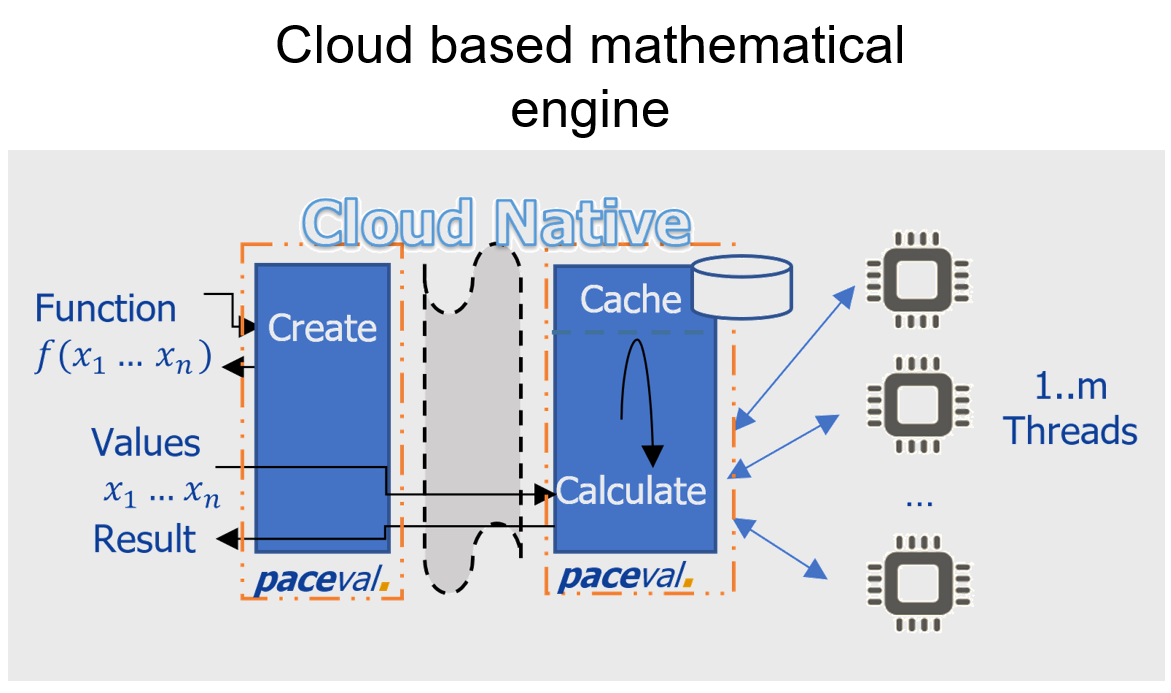
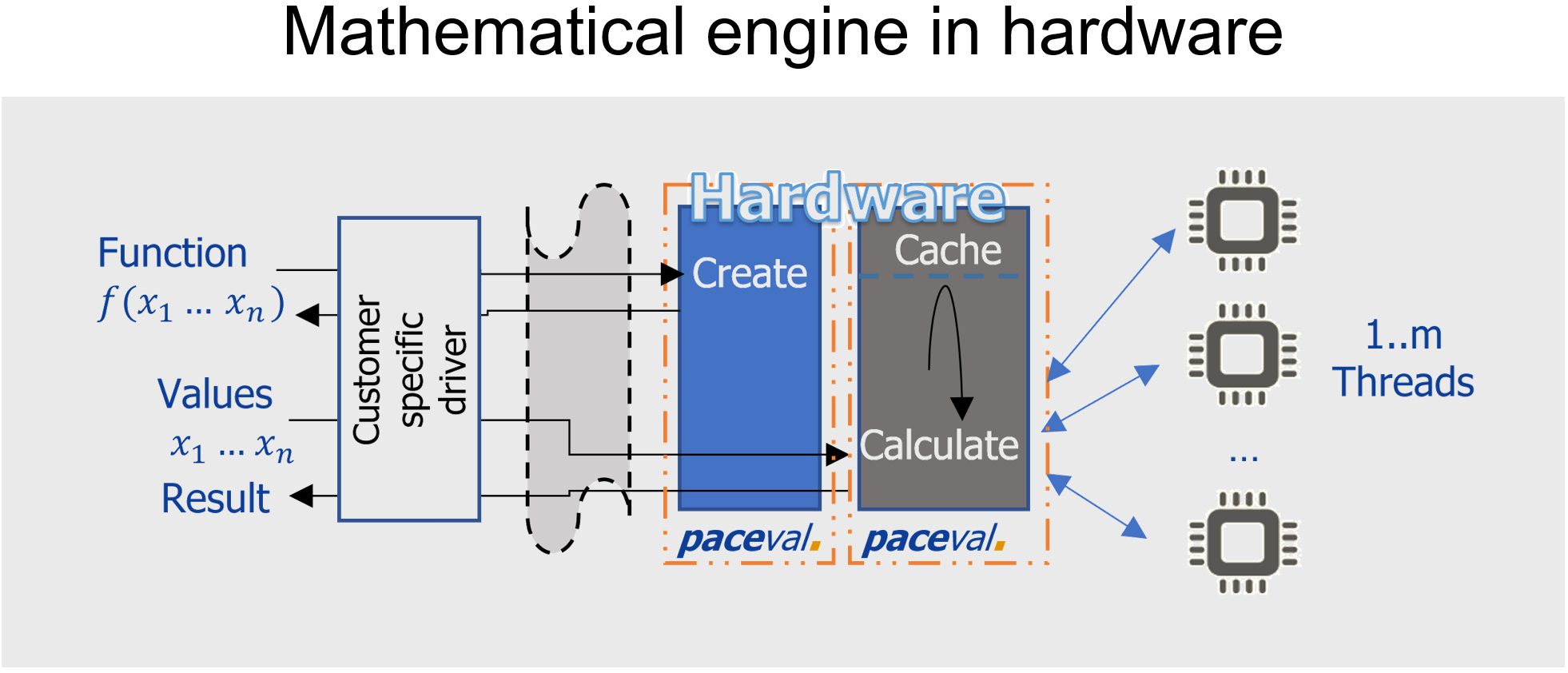
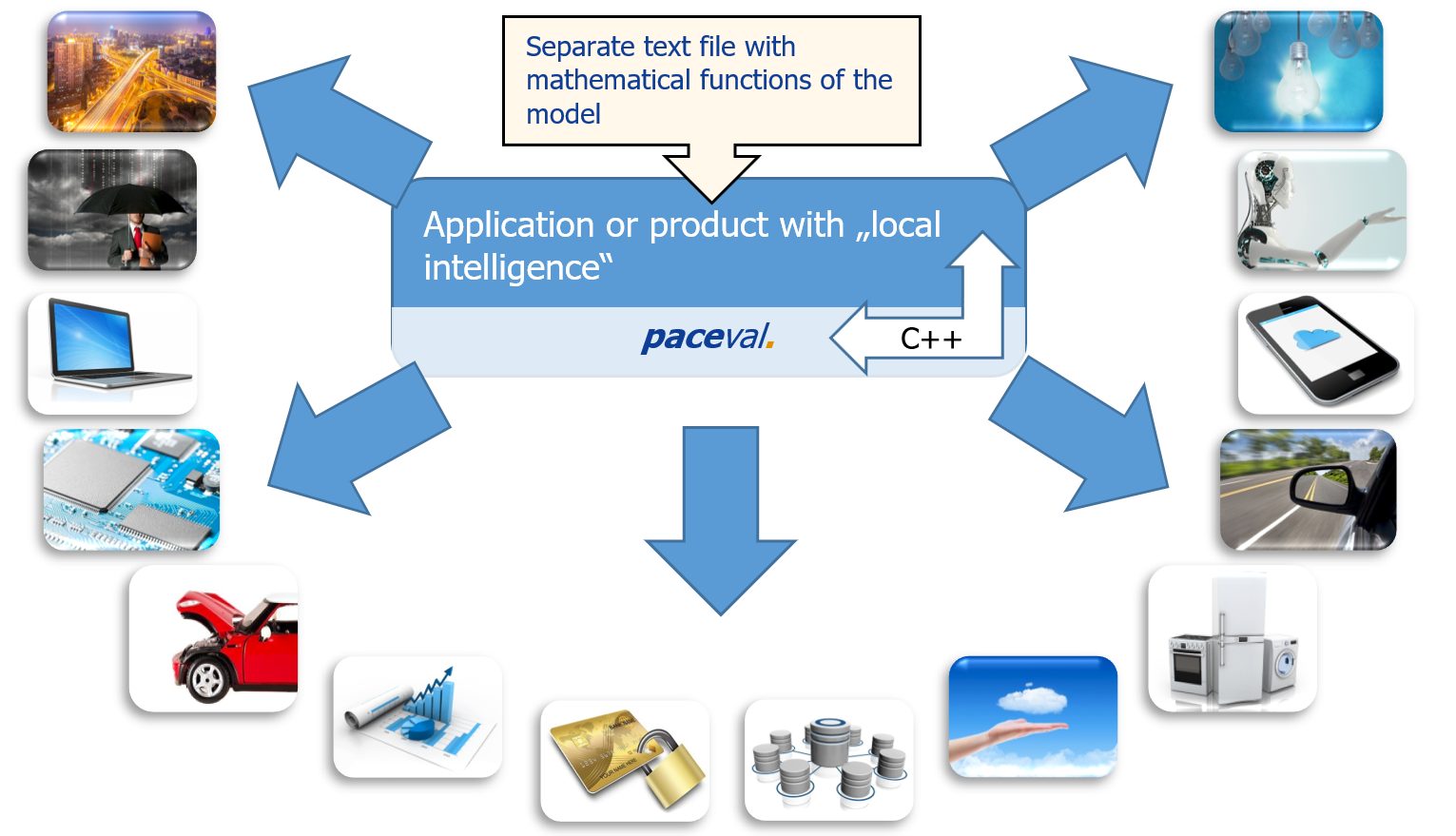
The process serves to provide various possibilities of software and hardware implementation. Fig. Software mathematical engine shows the reference implementation of our Windows Software Development Kit (SDK) which distributes step „Calculate“ on all available processor cores (CPUs and/or GPUs) inside the system. Fig. Cloud based mathematical engine und Fig. Mathematical engine in hardware show further variations, although steps „Create“ and „Calculate“ are separated logically and/or physically. Fig. Cloud based mathematical engine represents a very fast calculation server which is maximally scaled through Kubernetes (see our Github Guide for deploying the Kubernetes native paceval-service on any cluster). This is our paceval-server for INTEL/AMD and ARM64 as docker container (see our Github Mathematical Engine as a Service).
You are free to invent and implement any further applications.
Program code of paceval. compared to standard
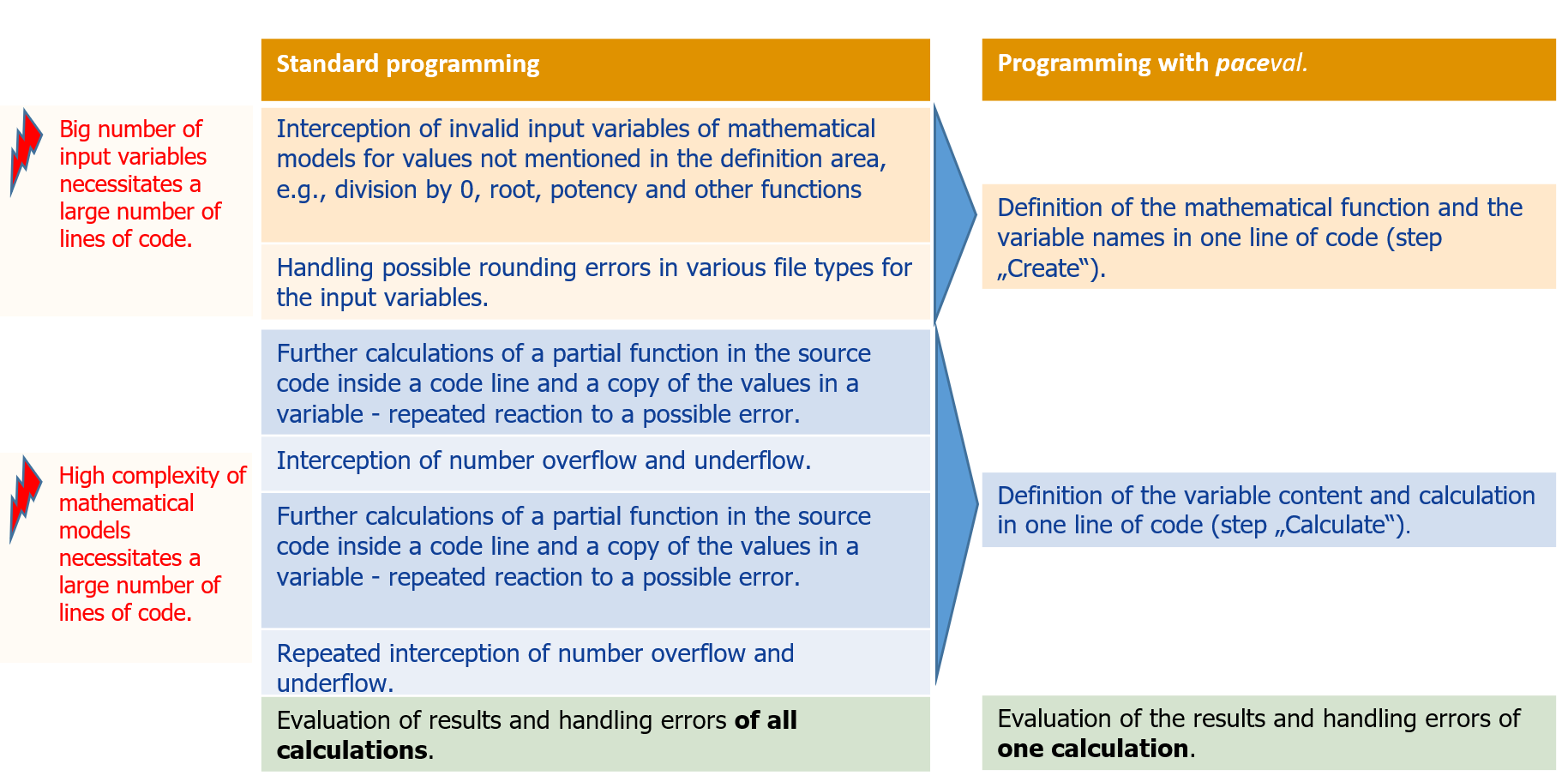
Standard programming requires significant effort to perform all possible calculations and correct the rounding errors.
Thanks to its simple and efficient program interface, paceval. helps you to reduce the amount of source code.
The effort of standard programming to handle mathematical calculations is huge. This effort significantly increases, as the number and complexity of the mathematical models and the number of input variables grow. The risk of an error and the costs of correcting abnormal behaviours of a program grow as well.
The effort required by paceval. is very small. The mathematical calculations are readable and easy to maintain or enhance. The low volume of program code reduce the risk of error and maintenance effort.
How does paceval. work in terms of speed?
paceval. calculates closed mathematical functions of any length and with any number of variables within milliseconds and irrespective of the system used.
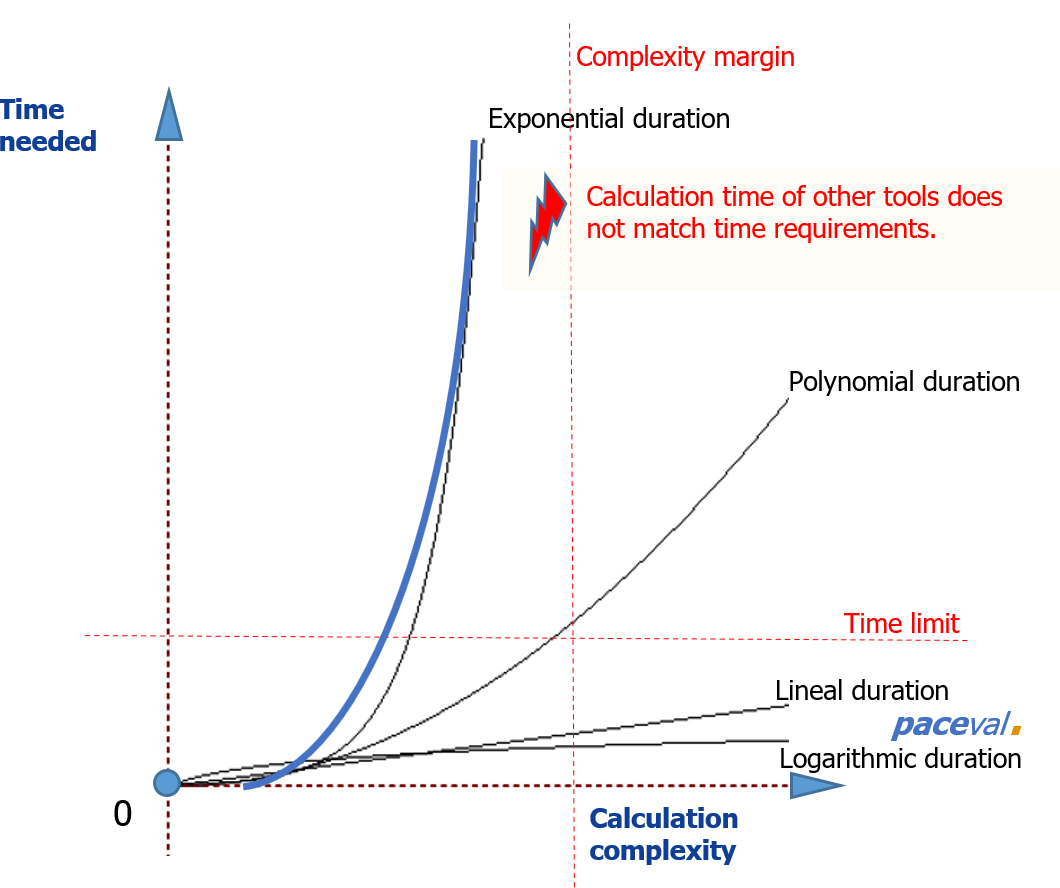
This is possible thanks to the unique mathematical parser with multiple caching. During partial calculations, a logarithmic duration can be achieved.
The more complex the calculation query, the longer is the required time period.
Scientific programs, engineering software, standard industry solutions, commonly used databases or proprietary calculation programs usually require polynomial or even exponential time. Complex calculations take too much time or sometimes cannot be processed at all. Proprietary codes of common engineering software use lineal duration, which does not offer flexibility or further duration optimization and need maintenance.
Eventually, only paceval. can be integrated with any software as a module and is compatible with small processors due to the small program size.
How does paceval. work in terms of precision?
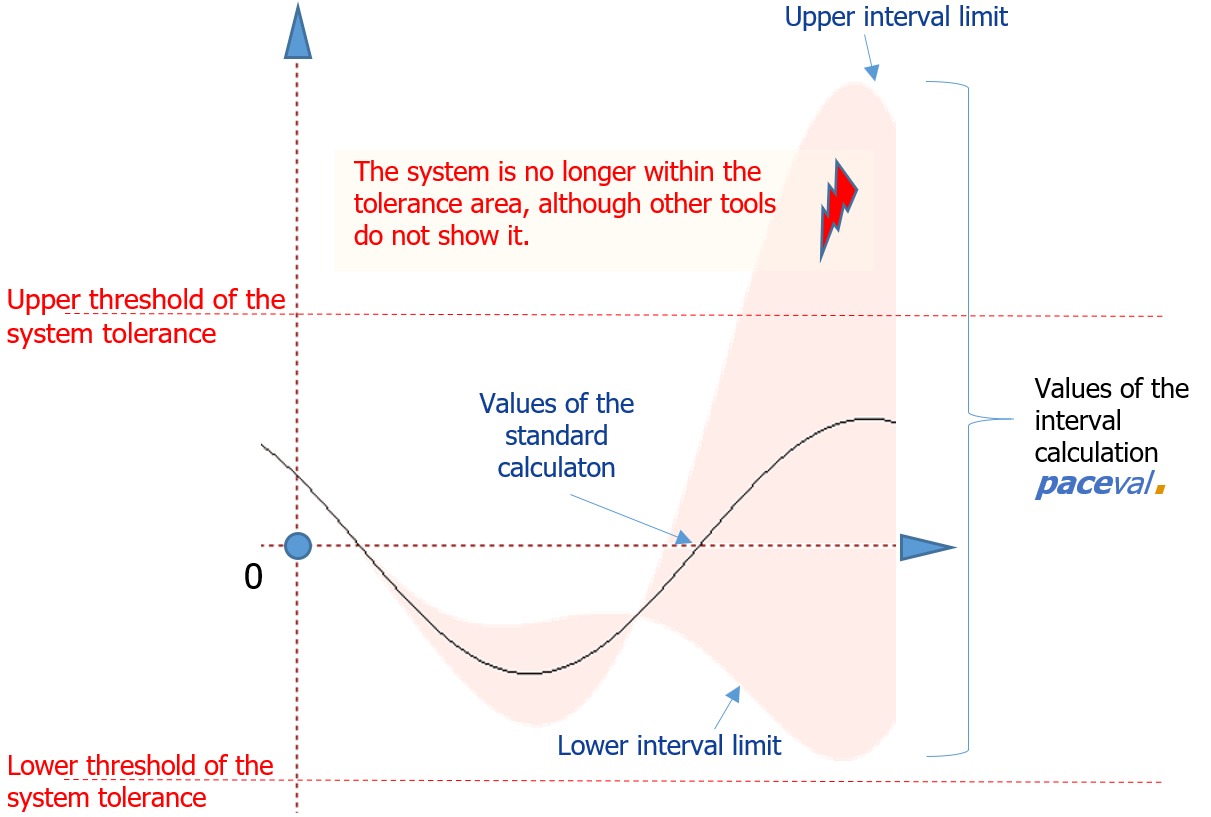
Computers cannot guarantee mathematical precision. Precision of calculation depends on the platform used, and each partial calculation may entail rounding errors. paceval. takes care of them by applying the “trusted interval computing“ (TINC) method. This way, it ensures that tolerance limits of the system are observed.
Depending on the given platform, paceval. provides internal calculations with the precision of up to 19 decimal places, and delivers additionally standard calculation value with upper and lower interval limits in which the true calculation value is enclosed.
The more complex the mathematical model, the more important is precision. In general, however, precision can be dependent on and reduced by the complexity of the underlying mathematical models, such as the length of functions and the number of variables.
It is, therefore, often reasonable to define the maximal calculation error in a timely fashion. Only then can you decide, if the outcome, the system or the product operates within the tolerance area – and take relevant measures.
paceval. makes it possible to define the outcome intervals in all mathematical partial calculations. Compared to other solutions, this approach allows to achieve unique degree of calculation precision.
Does paceval. set limitations in terms of functions?
Unlike other tools, paceval. sets no limitations to the length of a function and the number of variables.
All closed mathematical functions can be calculated, and the most important logical operators can be used together. This way, you can represent all closed financial, stochastic, engineering and scientific functions and also all models for machine learning.
With a source code license, you can even add further functions or operations.
You can simply use the common mathematical syntax. Generally, designers‘ mathematical models can be directly adopted and, as a separate source code, be readable and easy to maintain.
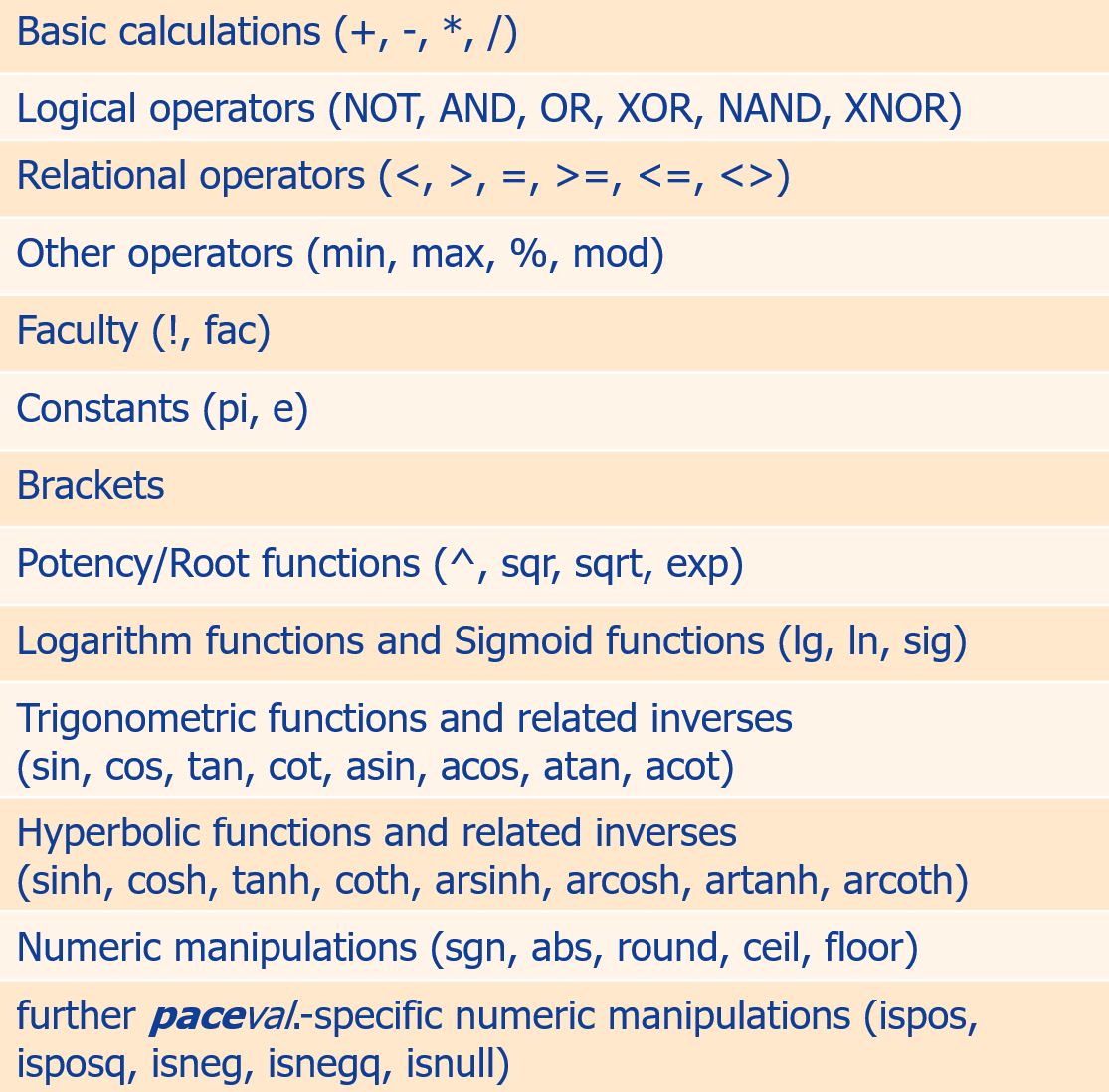
paceval. supports the following operations and partial functions:
Why can I easily and flexibly integrate paceval.?
paceval. is written using C++ and needs no further licenses. Thanks to its slim interface and low programming effort, it can instantly run on the most important computer systems. Its simple interface allows for the use of all current programming languages (e.g., Golang, Python, Cobol, Fortran, Java, Pascal, C# or Erlang). By separating the program logic from the calculating capability, the program memory is reduced, and expensive downtime can be avoided.
Using paceval., your applications can be equipped with mathematical models applicable to your system within a short time and with the lowest possible programming effort.
The mathematical functions can be saved separately from the application and can be optimized while the application is running without having to change or restart the application. This allows for creating high availability distributed systems. The mathematical model can simply be copied for the target platforms.
This way, there is more time to create prototypes for innovative concepts, demos or optimization purposes.